Answer:
Explanation:
so when the height is zero, that's when the rocket hits the ground. The equation will have two zeros, but one would be for a negative time, or before the rocket is launched. so we only one the one after the rocket is launched.
use the quadratic formula to solve for x ( which is time)
-124 +- sqrt [
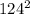 - 4*(-16)*(127) ] / 2 (-16)
- 4*(-16)*(127) ] / 2 (-16)
-124 +- sqrt [15376 + 8128 ] / -32
-124 +- sqrt [23504 ] / -32
-124 +- 153.310 / -32
if we take the positive part it will become the negative time so skip that one try the negative part 1st
-124 - 153.310 / -32
-277.310 / -32
8.6659 seconds to hit the ground. ( time of flight) aka TOF
8.67 seconds ( rounded to nearest 100th)