Question

A 200 g load attached to a horizontal spring moves in simple harmonic motion with a period of 0.410 s. The total mechanical energy of the spring–load system is 2.00 J.

Answer 1

Complete question:

A 200 g load attached to a horizontal spring moves in simple harmonic motion with a period of 0.410 s. The total mechanical energy of the spring–load system is 2.00 J. Find

(a) the force constant of the spring and (b) the amplitude of the motion.

Answer:

(a) the force constant of the spring = 47 N/m

(b) the amplitude of the motion = 0.292 m

Step-by-step explanation:

Given;

mass of the spring, m = 200g = 0.2 kg

period of oscillation, T = 0.410 s

total mechanical energy of the spring, E = 2 J

The angular speed is calculated as follows;

`\omega = (2\pi)/(T) \\\\\omega = (2\pi)/(0.41) \\\\\omega = 15.33 \ rad/s`

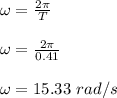
(a) the force constant of the spring

`\omega = \sqrt{(k)/(m) } \\\\\omega^2 = (k)/(m) \\\\k = m \omega^2\\\\k = (0.2)(15.33)^2\\\\k = 47 \ N/m`

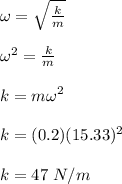
(b) the amplitude of the motion

E = ¹/₂kA²

2E = kA²

A² = 2E/k

`A = \sqrt{(2E)/(k) } \\\\A = \sqrt{(2* 2)/(47) }\\\\A = 0.292 \ m`