Question

Find the possible value of "a" using the distance formula.
(4,-1) and (a,5) with d = 10

Answer 1

`a=12\text{ or } -4`

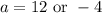
Explanation:

The distance formula is given by:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

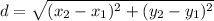
We are given the two points (4, -1) and (a, 5). The distance between them is 10.

Let (4, -1) be (x₁, y₁) and let (a, 5) be (x₂, y₂). Substitute:

`10=√((a-4)^2+(5-(-1))^2)`

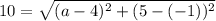
Solve for a. Square both sides and simplify:

`100=(a-4)^2+(6)^2`

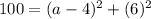
Simplify:

`64=(a-4)^2`

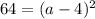
Take the square root of both sides. Since we are taking an even root, we will need plus/minus. Hence:

`\pm√(64)=\pm8=a-4`

Solve for a:

`a-4=8\Rightarrow a=12\text{ or } a-4=-8\Rightarrow a=-4`

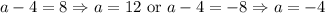
So, our two possible points are (12, 5) or (-4, 5).