Answer:
Center: (-1,-3)
Radius: 4.12 units
Explanation:
Hi there!
1) Find the center of the circle
When given two diameter endpoints, we can find the center of the circle by calculating for the midpoint since the center lies in the middle of the points:
Midpoint:
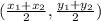 where the two points are
where the two points are
 and
and

Plug in the diameter endpoints (3,-2) and (-5,-4)
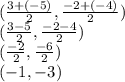
Therefore, the circle is centered at (-1,-3).
2) Find the radius of the circle
The radius of a circle is the distance between the outside edge and the center. We can find the radius by calculating for the distance between the center of the circle and one of the diameter endpoints.
Distance formula:
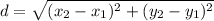 where the two points are
where the two points are
 and
and

Plug in the center (-1,-3) and a diameter endpoint (3,-2)
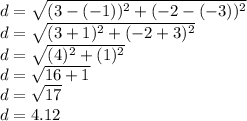
Therefore, the radius of the circle is approximately 4.12 units when rounded to the nearest hundredth.
I hope this helps!