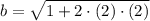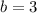Answer:
The family of all prime numbers such that
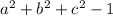 is a perfect square is represented by the following solution:
is a perfect square is represented by the following solution:
 is an arbitrary prime number. (1)
is an arbitrary prime number. (1)
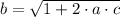 (2)
(2)
 is another arbitrary prime number. (3)
is another arbitrary prime number. (3)
Explanation:
From Algebra we know that a second order polynomial is a perfect square if and only if
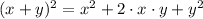 . From statement, we must fulfill the following identity:
. From statement, we must fulfill the following identity:

By Associative and Commutative properties, we can reorganize the expression as follows:
 (1)
(1)
Then, we have the following system of equations:
 (2)
(2)
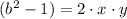 (3)
(3)
 (4)
(4)
By (2) and (4) in (3), we have the following expression:
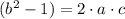

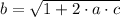
From Number Theory, we remember that a number is prime if and only if is divisible both by 1 and by itself. Then,
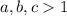 . If
. If
 ,
,
 and
and
 are prime numbers, then
are prime numbers, then
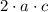 must be an even composite number, which means that
must be an even composite number, which means that
 and
and
 can be either both odd numbers or a even number and a odd number. In the family of prime numbers, the only even number is 2.
can be either both odd numbers or a even number and a odd number. In the family of prime numbers, the only even number is 2.
In addition,
 must be a natural number, which means that:
must be a natural number, which means that:
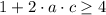

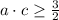
But the lowest possible product made by two prime numbers is
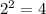 . Hence,
. Hence,
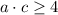 .
.
The family of all prime numbers such that
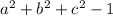 is a perfect square is represented by the following solution:
is a perfect square is represented by the following solution:
 is an arbitrary prime number. (1)
is an arbitrary prime number. (1)
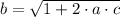 (2)
(2)
 is another arbitrary prime number. (3)
is another arbitrary prime number. (3)
Example:
 ,
,