Solution :
Given data:
Area of the solar sail, A = 16
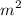
Mass (array + sail), m =
 kg
kg
Power, P = 100 GW
=
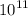 W
W
Time, t = 10 min
= 10 x 60 s
Distance, D =
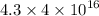 m
m
Kinetic energy,
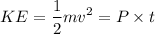
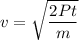
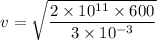
 m/s
m/s
So, the acceleration is
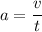
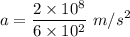
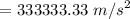
Therefore, force,

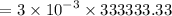
= 1000 N
Pressure,

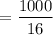
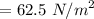
Therefore, time taken is t
Now the distance is
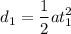
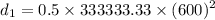
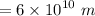
Now, the distance,

Now,

= 859999700 s
Therefore, total time is
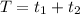
= 86000300 s
= 27.27 years