Question

A national organization has been working with utilities throughout the nation to find sites for large wind machines that generate electricity. Wind speeds must average more than 20 miles per hour (mph) for a site to be acceptable. Recently, the organization conducted wind speed tests at a particular site. Based on a sample of n = 43 wind speed recordings (taken at random intervals), the wind speed at the site averaged x = 25.8 mph, with a standard deviation of s = 4.2 mph. To determine whether the site meets the organization's requirements, consider the test, H0: µ = 25 vs. Ha: µ > 25, where µ is the true mean wind speed at the site and alpha = .01. Suppose the value of the test statistic were computed to be 1.25. State the conclusion.

A) At alpha = .01, there is sufficient evidence to conclude the true mean wind speed at the site exceeds 25 mph.
B) At alpha΅= .01, there is insufficient evidence to conclude the true mean wind speed at the site exceeds 25 mph.
C) We are 99% confident that the site meets the organization's requirements.
D) We are 99% confident that the site does not meet the organization's requirements.

Answer 1

B) At alpha = 0.01, there is insufficient evidence to conclude the true mean wind speed at the site exceeds 25 mph.

Explanation:

P-value of the test:

The p-value of the test is the probability of finding a sample mean above 25.

We are using the t-distribution, with test statistic t = 1.25 and 43 - 1 = 42 degrees of freedom. This probability is a right-tailed test.

With the help of a calculator, this p-value is of 0.1091.

Since the p-value of the test is 0.1091 > 0.01, at
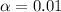`\alpha = 0.01` there is insufficient evidence to conclude the true mean wind speed at the site exceeds 25 mph, and the correct answer is given by option B.