Question

1. Consider three dielectric media with flat and parallel boundaries with refractive indices n1, n2, and n3. Show that for normal incidence the reflection coefficient between layers 1 and 2 is the same as that between layers 2 and 3 if n2 = √[n1n3]. What is the significance of this?

2. Consider a Si photodiode that is designed for operation at 900 nm. Given a choice of two possible antireflection coatings, SiO2 with a refractive index of 1.5 and TiO2 with a refractive index of 2.3 which would you use and what would be the thickness of the antireflection coating? The refractive index of Si is 3.5. Explain your decision.

Answer 1

1) r12 = r23 ( This signifies that the waves interfere destructively )

2) SiO2 should be chosen , Thickness = 150 nm

Step-by-step explanation:

1 ) Prove that; r12 = r23

i) Considering light travelling in medium 1 ( i.e. incident between layers 1 and 2 )

r₁₂ ( reflection coefficient ) = ( n₁ - n₂ ) / ( n₁ + n₂ )

= ( n₁ - √n₁ n₃ ) / ( n₁ + √n₁ n₃ )

=
`\frac{1- \sqrt{(n3)/(n1) } }{1+ \sqrt{(n3)/(n1) } }`

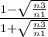
ii) considering light travelling in medium 2 ( i.e. incident between layers 2 and 3 )

r₂₃ ( reflection coefficient ) = ( n₂ - n₃ ) / (n₂ + n₃ )

= ( √n₁ n₃ - n₃ ) / ( √n₁ n₃ + n₃ )

=
`\frac{1- \sqrt{(n3)/(n1) } }{1+ \sqrt{(n3)/(n1) } }`

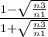
hence r12 = r23 ( This signifies that the waves interfere destructively )

2) Determine the antireflection coating to use and the thickness

Refractive index of SiO2 = 1.5

Refractive index of TiO2 = 2.3

an ideal refractive index for an antireflection coating ( n2 )

= √n₁ n₃ = √(1)(3.5) = 1.87

the refractive index closest to this value = 1.5 ( hence SiO2 will be chosen )

Thickness of SiO2 ( diameter )

= 900 / ( 4*n2 )

= 900 / ( 4 * 1.5 ) = 900 / 6 = 150 nm