Question

Chloe breaks into the pantry after Albert goes to work. She finds and opens a family-pack of mixed nuts. After surfing the web, she finds that these packs claim to be 20% almond (A), 30% cashew (C), 10% macadamia (M), and 40% peanut. Chloe discovers that her bag contains 14 almonds, 28 cashews, 6 macadamias, and 52 peanuts.

a) Perform an appropriate test to determine whether this claim is true or not at a = 0.05. State all the relevant steps (listed in exercise 1).
b) What is the decision and conclusion (write a sentence) at a = 0.1?
c) Chloe is a choosy and sneaky doggie. She likes to find a p-value first and then come up with a significance level, a later so she can reject as many Hos as possible. Is her method acceptable?

Answer 1

In this case we have to use
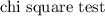`$\text{chi square test}$` for the goodness of fit.

Null hypothesis is :
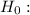`$H_0 :$` Data follows the given distribution

Alternate hypothesis is :
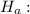`$H_a:$` Data do not follow the given distribution

The level of significance,
`$\alpha = 0.05$`

The test statistics is given by :

Chi square =
`$\sum((O-E)^2)/(E)$`

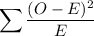
Here O is the observed frequencies

E is the expected frequencies

So we have, N = number of the categories = 4

df = degrees o freedom = N - 1

= 4 - 1 = 3

Critical value =
`$7.814727764$`

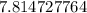
Calculating the table for the test statistics are given as :

Category prop. O E
`$((O-E)^2)/(E)$`

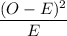
A 0.2 14 20 1.80

C 0.3 28 30 0.13

M 0.1 6 10 1.60

P 0.4 52 40 3.60

Total 1 100 100 7.13

The test statics = chi square =
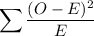`$\sum((O-E)^2)/(E)$` = 7.13

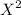`$X^2$` statistics = 7.13

P-value = 0.067767248

P -value >
`$\alpha = 0.05$`

Therefore, we do not reject the
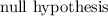`$\text{null hypothesis}$`. There is sufficient evidence to conclude that the data follows the given distribution. So there is sufficient evidence to conclude the given claim is true.