Question

Choose region 2 from the Explore & Test page that is bounded by the curves y = (x − 3)2 when x ≥ 3, x = 0, y = 4. Set the axis of revolution to be the y-axis and use the first slider to rotate the region around the y-axis. The solid generated resembles a coffee cup without a handle. Move the second slider to see how the volume of the disks can be used to approximate the volume of the coffee cup.

Answer 1

V= 76 π cubic units

Explanation:

y=
`(x-3)^(2)` ----->
`x=√(y) +3`

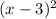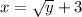
Here we will apply the risk method.

Risk method: consider a strip of length x and width dy as

a) Radius= R(y) = x =
`√(y) + 3`

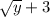
[We rotate this disc about y-axis to get a disk]

b) Cross-section area = A(y)= π
`(radius)^(2)`

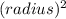
= A(y)= π (y+9+6
`√(y)`)

--------> Volume of the disc = A(y) x dy

c) Required volume= v =
`\int\limits^4_0` A(y) x d(y)

V=
`\int\limits^4_0` π (y + 9 + 6
`√(y)` ) dy

V= π [
`{(y^(2) )/(2) + 9y + 4y^{(3)/(2) }`
`]_(0) ^(4)`

V= 76 π cubic units.