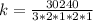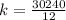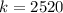Question

Use the Binomial Theorem to find the coefficient of x^3y^2z^5 in (x + y + z)^10.

Answer 1

The coefficient is 2520

Explanation:

Given

`(x + y + z)^{10`

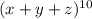
Required

The coefficient of
`x^3y^2z^5`

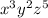
To do this, we make use of:

`k = (n!)/(n_1!n_2!....n_m!)`

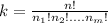
Where

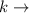`k \to` coefficient

`n = 10` the exponent of the given expression

`n_1=3` -- exponent of x

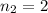`n_2=2` --- exponent of y

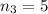`n_3=5` --- exponent of z

So, we have:

`k = (n!)/(n_1!n_2!....n_m!)`

`k = (10!)/(3!2!5!)`

Expand

`k = (10*9*8*7*6*5!)/(3!2!5!)`

`k = (10*9*8*7*6)/(3!2!)`

`k = (30240)/(3!2!)`

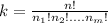
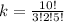
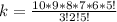
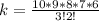
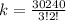
Expand the denominator

`k = (30240)/(3*2*1*2*1)`

`k = (30240)/(12)`

`k = 2520`