Question

We plan to choose a random sample of college students in Norman (OK) and Lubbock (TX) to examine how they spent their time on Friday evenings during the pandemic (from early April 2020 to late December 2020). Consider the population variable below: Cost of food, drink, and entertainment on a Friday evening. Let us assume that the population standard deviation is $12.5. Also, let us assume that we are willing to accept only a $1.5 margin of errors in our estimations. Level of confidence being set at 95%, how many observations do we need in order to estimate the population mean for the above cost?

Answer 1

267 observations are needed.

Explanation:

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.95)/(2) = 0.025`

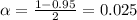
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
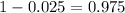`1 - 0.025 = 0.975`, so Z = 1.96.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

Let us assume that the population standard deviation is $12.5.

This means that
`\sigma = 12.5`

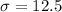
Willing to accept only a $1.5 margin of errors in our estimations. How many observations do we need in order to estimate the population mean for the above cost?

This is n for which M = 1.5. So

`M = z(\sigma)/(√(n))`

`1.5 = 1.96(12.5)/(√(n))`

`1.5√(n) = 1.96*12.5`

`√(n) = (1.96*12.5)/(1.5)`

`(√(n))^2 = ((1.96*12.5)/(1.5))^2`

`n = 266.8`

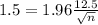
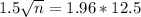
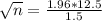
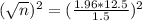
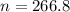
Rounding up:

267 observations are needed.