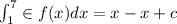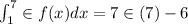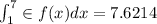Answer:
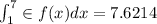
Explanation:
From the question we are told that:
Definite integral
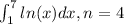
Generally the equation for Trapezoidal Rule is mathematically given by
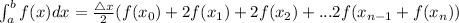
Where
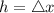
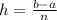
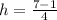
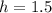
Therefore
For
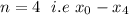
The Endpoints are
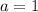
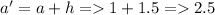
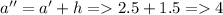
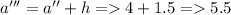
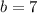
Evaluating trapezoidal function at endpoints
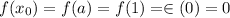
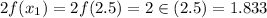
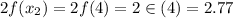
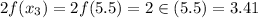
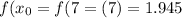
Therefore approximation of the integral
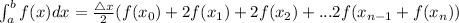
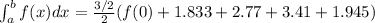
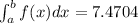
b)
Generally the equation for Simpson,s Rule is mathematically given by
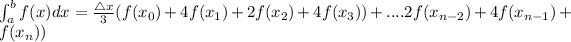
Where

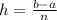
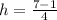
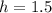
Therefore
For
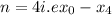
The Endpoints are
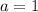
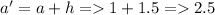
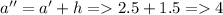
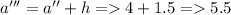
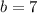
Evaluating trapezoidal function at endpoints
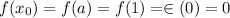
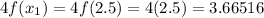
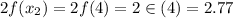
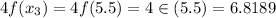
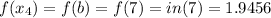
Therefore
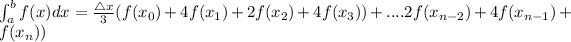
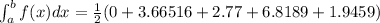
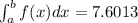
Therefore shown graphing utility