Question

TV advertising agencies face increasing challenges in reaching audience members because viewing TV programs via digital streaming is gaining in popularity. A poll reported that 56% of 2348 American adults surveyed said they have watched digitally streamed TV programming on some type of device.

a. Calculate and interpret a confidence interval at the 99% confidence level for the proportion of all adult Americans who watched streamed programming up to that point in time.
b. What sample size would be required for the width of a 99% CI to be at most .05 irrespective of the value P?

Answer 1

a)

The 99% confidence interval for the proportion of all adult Americans who watched streamed programming up to that point in time is (0.5336, 0.5864). This means that we are 99% sure that the true proportion of all adult Americans who watched streamed programming up to that point in time is between these two values.

b)

A sample size of 664 is required.

Explanation:

Question a:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

A poll reported that 56% of 2348 American adults surveyed said they have watched digitally streamed TV programming on some type of device.

This means that
`\pi = 0.56, n = 2348`

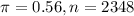
99% confidence level

So
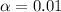`\alpha = 0.01`, z is the value of Z that has a p-value of
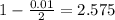`1 - (0.01)/(2) = 2.575`, so
`Z = 2.575`.

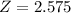The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.56 - 2.575\sqrt{(0.56*0.44)/(2348)} = 0.5336`

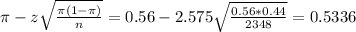
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.56 + 2.575\sqrt{(0.56*0.44)/(2348)} = 0.5864`

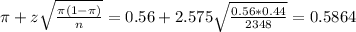
The 99% confidence interval for the proportion of all adult Americans who watched streamed programming up to that point in time is (0.5336, 0.5864). This means that we are 99% sure that the true proportion of all adult Americans who watched streamed programming up to that point in time is between these two values.

b. What sample size would be required for the width of a 99% CI to be at most .05 irrespective of the value P?

The margin of error is of:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

This sample size is given by n, with
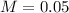`M = 0.05` and
`\pi = 0.5`.

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.05 = 2.575\sqrt{(0.5*0.5)/(n)}`

`0.05√(n) = 2.575*0.5`

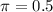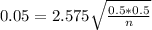
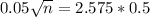
Dividing both sides by 0.05.

`√(n) = 2.575*10`

`(√(n))^2 = (2.575*10)^2`

`n = 663.1`

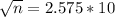
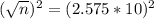
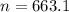
Rounding up:

A sample size of 664 is required.