Answer:
The planning value for the population standard deviation is of 4330.
Explanation:
Uniform probability distribution:
The uniform probability distribution has two bounds, a and b. The standard deviation is given by:
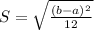
Annual starting salaries for college graduates with degrees in business administration are generally expected to be between 20000 and 35000.
Uniform in this interval, so
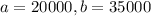
What is the planning value for the population standard deviation?

The planning value for the population standard deviation is of 4330.