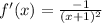Question

Identify each expression that represents the slope of a tangent to the curve y=1/x+1 at any point (x,y) .

Answer 1

The asker is talking about this question (see pic)

Answer 2

Slope of a tangent to the curve =
`f'(x) = (-1 )/((x+1)^(2) )`

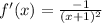
Explanation:

Given - y = 1/x+1

To find - Identify each expression that represents the slope of a tangent to the curve y=1/x+1 at any point (x,y) .

Proof -

We know that,

Slope of tangent line = f'(x) =
`\lim_(h \to 0) (f(x+h) - f(x))/(h)`

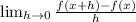
We have,

f(x) = y =
`(1)/(x+1)`

So,

f(x+h) =
`(1)/(x+h+1)`

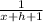
Now,

Slope = f'(x)

And

`f'(x) = \lim_(h \to 0) (f(x+h) - f(x))/(h) \\= \lim_(h \to 0) ((1)/(x+h+1) - (1)/(x+1) )/(h)\\= \lim_(h \to 0) (x+1 - (x+h+1) )/(h(x+1)(x+h+1))\\= \lim_(h \to 0) (x +1 - x-h-1 )/(h(x+1)(x+h+1))\\= \lim_(h \to 0) (-h )/(h(x+1)(x+h+1))\\= \lim_(h \to 0) (-1 )/((x+1)(x+h+1))\\= (-1 )/((x+1)(x+0+1))\\= (-1 )/((x+1)(x+1))\\= (-1 )/((x+1)^(2) )`

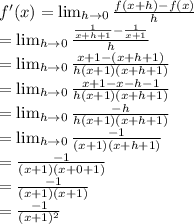
∴ we get

Slope of a tangent to the curve =
`f'(x) = (-1 )/((x+1)^(2) )`