Question

Evaluate and input the result of the following integral.

∫ Fdr= ?
c

F=

Answer 1

∫ F dr= 1

c

Explanation:

The correct question is -

Given -
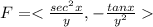`F = < (sec^(2) x)/(y) , - (tan x)/(y^(2) )>` and C : (0, 1) to
`((\pi )/(4) , 1)`

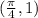
To find - Evaluate and input the result of the following integral.

Proof -

We know that,

dr = dx i + dy j

F = < F1, F2 >

Now, we know

`d((tanx)/(y )) = (d)/(dx)((tanx)/(y)) + (d)/(dy)((tanx)/(y))`

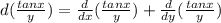
So,

`(d)/(dx)((tanx)/(y)) =(1)/(y) (d)/(dx)({tanx}) \\\\ = (sec^(2) x)/(y) \\(d)/(dy)((tanx)/(y)) = tanx (d)/(dy)(y^(-1)) \\ = -(tanx)/(y^(2) )`

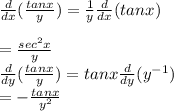
Now,

We can see that,

`d((tanx)/(y )) = (sec^(2) x)/(y) dx - ((tanx)/(y^(2) ))dy`

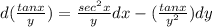
So,

`\int\limits^{}_C {F. dr} = \int\limits^{}_C d((tanx)/(y) )\\= [(tanx)/(y) ]\limits^{((\pi )/(4) ,1)}_((0,1))\\= [(tanx)/(y) ]\limits^{}_{((\pi )/(4) ,1)} - [(tanx)/(y) ]\limits^{}_((0,1))\\= (tan((\pi )/(4) ))/(1) - (tan 0)/(1)\\= 1 - 0\\= 1`

∴ we get

∫ F dr= 1

c