Question

Four equivalent forms of a quadratic function are given. Which form displays the zeros of function h?

Answer 1

`h(x) = -4(x - 2)(x + 2)`

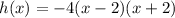
Explanation:

Given

`h(x) = -4(x - 2)(x + 2)`

`h(x) = -2(2x^2 - 8)`

`h(x) = -4(x^2 - 4)`

`h(x) = -4x^2 + 16`

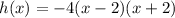
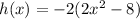
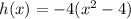
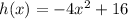
Required

Which shows the zeros of h(x)

To determine the zeros of a function, the function must be written as:

`h(x) = n(x \± a)(x \± b)`

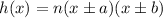
Where

`n \\e 0`

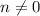
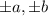`\± a,\± b` are the zeros

Of options (a) to (d), only (a) is written in the form:

`h(x) = n(x \± a)(x \± b)`

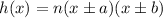
i.e.

`h(x) = -4(x - 2)(x + 2)`

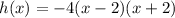
Other options do not show the zeros