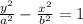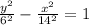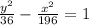Answer:
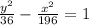
Explanation:
From the question we are told that:
Vertices of hyperbola at
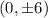
Asymptotes at
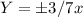
Generally the expression for Vertices of hyperbola is mathematically given by
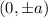
Therefore
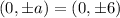
Comparing variables
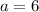
Generally the expression for Asymptotes of hyperbola is mathematically given by
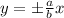
Therefore
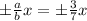
Therefore
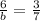
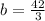
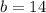
Generally the equation for Hyperbola of hyperbola is mathematically given by