Answer:
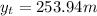
Step-by-step explanation:
Para resolver este problema debemos contemplar dos tramos.
En el primer tramo, la fuerza aplicada impulsa al cuerpo a subir una altura dada debido a la aceleración que genera esa fuerza.
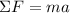
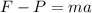
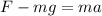
En donde:
F: es la fuerza aplicada = 60 N
P: es el peso del cuerpo = mg
m: es la masa del cuerpo = 4 kg
g: es la aceleración debido a la gravedad = 9.81 m/s²
a: es la aceleración
Entonces, la aceleración generada por la fuerza aplicada es:
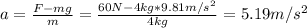
Ahora, debemos calcular la altura recorrida mientras el cuerpo está acelerado hacia arriba:
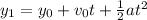
En donde:
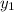 : es la altura final del tramo 1 =?
: es la altura final del tramo 1 =?
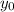 : es la altura inicial = 0
: es la altura inicial = 0
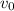 : es la velocidad inicial = 0 (parte del reposo)
: es la velocidad inicial = 0 (parte del reposo)
t: es el tiempo = 8 s
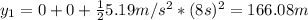
Por lo tanto, mientras el cuerpo está acelerado (durante los 8 s) recorre 166.08 metros.
Ahora, en el segundo tramo el cuerpo sigue subiendo hasta alcanzar una altura máxima para luego comenzar a descender. Podemos usar la siguiente ecuación para calcular la altura recorrida.
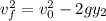
En donde:
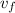 : es la velocidad final = 0 (en la altura máxima)
: es la velocidad final = 0 (en la altura máxima)
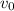 : es la velocidad inicial
: es la velocidad inicial
Primero debemos encontrar la velocidad inicial en el segundo tramo, que es igual a la velocidad final del primer tramo:
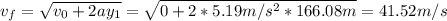
Entonces, la altura recorrida en el segundo tramo es:
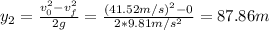
Finalmente, la altura máxima es:
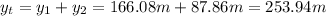
Espero que te sea de utilidad!