Question

The polynomial degree 3, P(x), has a root of multiplicity 2 at x = 5 and a root of multiplicity 1 at x = -1. The y-intercept is y = -10.

Find a formula for P(x).

Answer 1

`P(x) = -0.4(x^3 - 9x^2 + 15x + 25)`

Explanation:

Zeros of a function:

Given a polynomial f(x), this polynomial has roots
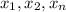`x_(1), x_(2), x_(n)` such that it can be written as:
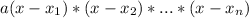`a(x - x_(1))*(x - x_(2))*...*(x-x_n)`, in which a is the leading coefficient.

Root of multiplicity 2 at x = 5 and a root of multiplicity 1 at x = -1.

This means that
`x_1 = x_2 = 5, x_3 = -1`

So

`P(x) = a(x - x_(1))*(x - x_(2))*(x-x_3)`

`P(x) = a(x - 5)*(x - 5)*(x-(-1))`

`P(x) = a(x-5)^2(x+1)`

`P(x) = a(x^2 - 10x + 25)(x+1)`

`P(x) = a(x^3 - 9x^2 + 15x + 25)`

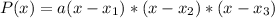
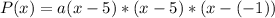
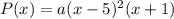
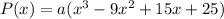
The y-intercept is y = -10.

This means that when
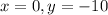`x = 0, y = -10`. We use this to find a.

`P(x) = a(x^3 - 9x^2 + 15x + 25)`

`-10 = 25a`

`a = -(10)/(25)`

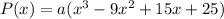
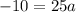
`a = -0.4`. So

`P(x) = -0.4(x^3 - 9x^2 + 15x + 25)`