Given:
The equation of parallel line is:
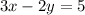
The required line passing through the midpoint of the line segment joining the points (-4,2) and (2,4).
To find:
The equation of required line.
Solution:
Midpoint of line segment joining the points (-4,2) and (2,4) is:
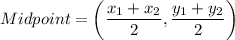
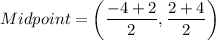
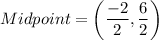
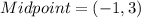
It means the required line passes through the point (-1,3).
The slope of line
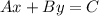 is:
is:
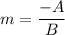
The given equation is:
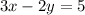
Here, A=3 and B=-2. So, the slope of the line is:
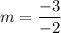

Slope of parallel lines are same. So, the slope of the required line is 1.5.
The required line passes through the point (-1,3) with slope 1.5. So, the equation of the line is:
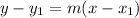
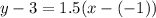
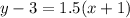

Adding 3 on both sides, we get
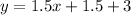

Therefore, the equation of the required line is
 .
.