Question

A fair coin is flipped 3 times. Let X be the number of heads in the 3 tosses，and Y be the absolute value of difference between heads and tailes. Find E(X)and E(Y)，respectively.

Answer 1

E(X) = 1.5, E(Y) = 0

Explanation:

For each coin, there are only two possible outcomes. Either it is heads, or it is tails. The probability of a toss being heads or tails is independent of any other toss. This means that we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

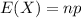
A fair coin is flipped 3 times.

3 times means that
`n = 3`

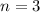
Fair coin means that it is equally as likely to be heads or tails, so
`p = 0.5`

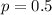
Find E(X)

`E(X) = np = 3*0.5 = 1.5`

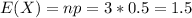
Find E(Y)

The expected number of heads, E(X) is 1.5. Since the coin is fair, the expected number of tails is also 1.5. Thus, the absolute value of the difference between heads and tails is:

E(Y) = 1.5 - 1.5 = 0