Question

the area of a square whose sides have length x cm is increasing at the rate of 12cm²/s. how fast is the length of a side increasing when the area is 81cm²​

Answer 1

0.67 cm/s

Explanation:

The area of a square is given by :

`A=x^2` ....(1)

Where

x is the side of a square

`(dA)/(dt)=12\ cm^2/s`

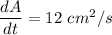
Differentiating equation (1) wrt t.

`(dA)/(dt)=2x* (dx)/(dt)`

When A = 81cm²​, the side of the square, x = 9 cm

Put all the values,

`12=2* 9* (dx)/(dt)\\\\(dx)/(dt)=(2)/(3)\\\\(dx)/(dt)=0.67\ cm/s`

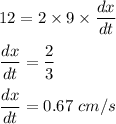
So, the length of the side of a square is changing at the rate of 0.67 cm/s.