Question

1

How does the graph of g(x) =
X+4
-6
compare to the graph of the parent function RX)=
- ?
g(x) is shifted 4 units right and 6 units up from f(x).
O g(x) is shifted 4 units right and 6 units down from f(x).
g(x) is shifted 4 units left and 6 units up from f(x).
O g(x) is shifted 4 units left and 6 units down from f(x).

Answer 1

g(x) is shifted 4 units left and 6 units down from f(x).

Explanation:

The parent function is:

f(x).

The child function is:

`g(x) = f(x+4) - 6`

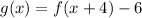
Transformation 1:

`g(x) = f(x+4)`

Shifting a function f(x) a units to the left is finding f(x + a). So g(x) = f(x + 4) is f(x) shifted 4 units to the left.

Transformation 2:

`g(x) = f(x+4) - 6`

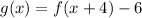
Subtracting a function f(x) by a constant a is the same as shifting the function a units down. So subtracting by 6 is shifting the function 6 units down. Thus, the correct answer is:

g(x) is shifted 4 units left and 6 units down from f(x).