Answer:
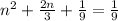 --- Trinomial
--- Trinomial
 --- Binomial
--- Binomial
Explanation:
Given

Solving (a): Perfect square trinomial
We have:

Express as an equation
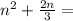
Start----------------------------
Take coefficient of n i.e. (2/3)
Half it: i.e. (1/3)
Square it: (1/63^2
Add to both sides of the equation
---------------------------End
So, we have:
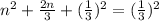
Remove brackets
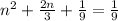
Solving (b): Binomial Squared
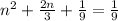
Expand
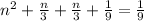
Factorize:
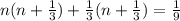
Factor out n + 1/3
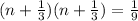
Express as square
