Answer:
a) 0.3483 = 34.83% probability that 369 or more of the 1478 adults have sleepwalked.
b) 369 < 403.4, which means that 369 is less than 2.5 standard deviations above the mean, and thus, a result of 369 is not significantly high.
c) Since the sample result is not significant, it suggests that the rate of 24.5% is a good estimate for the percentage of people that have sleepwalked.
Explanation:
We use the normal approximation to the binomial to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
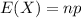
The standard deviation of the binomial distribution is:

A result is considered significantly high if it is more than 2.5 standard deviations above the mean.
Normal probability distribution
Problems of normally distributed distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that
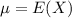 ,
,
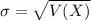 .
.
Assume that 24.5% of people have sleepwalked.
This means that
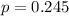
Sample of 1478 adults:
This means that
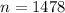
Mean and standard deviation:
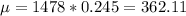
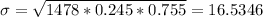
a. Assuming that the rate of 24.5% is correct, find the probability that 369 or more of the 1478 adults have sleepwalked.
Using continuity correction, this is
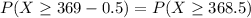 , which is 1 subtracted by the p-value of Z when X = 368.5.
, which is 1 subtracted by the p-value of Z when X = 368.5.

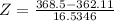

 has a p-value of 0.6517
has a p-value of 0.6517
1 - 0.6517 = 0.3483
0.3483 = 34.83% probability that 369 or more of the 1478 adults have sleepwalked.
b. Is that result of 369 or more significantly high?
362.11 + 2.5*16.5346 = 403.4
369 < 403.4, which means that 369 is less than 2.5 standard deviations above the mean, and thus, a result of 369 is not significantly high.
c. What does the result suggest about the rate of 24.5%?
Since the sample result is not significant, it suggests that the rate of 24.5% is a good estimate for the percentage of people that have sleepwalked.