Answer:
7,000,000
Explanation:
Limit of a function:
The limit of a function is finding looking at it's lateral limits.
If the lateral limits are equal:
The limit exists.
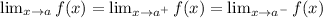
If lateral limits are different:
That is:
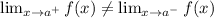 , then the limit does not exist.
, then the limit does not exist.
In this question:
To the left of 1, that is, 0.9999....
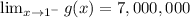
To the right of 1, that is, 1.0001...

Since the both limits are the same, the limits exists and it's value is of 7,000,000.