Concept,
Two chords with a shared termination point on the circle make an inscribed angle in a circle. The vertex of the angle is this shared terminal point. An inscribed angle is equal to half the length of the intercepted arc.
Given,
We have been given a figure in which the line
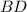 is the tangent to the circle at the point
is the tangent to the circle at the point
 and the measure of the arc
and the measure of the arc
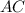 is
is
 . And also we have some options:
. And also we have some options:
A.

B.
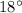
C.
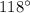
D.

To find,
We have to choose the correct option which tells the measure of the angle of
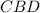 .
.
Solution,
In the figure, we can see that
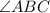 is an inscribed angle and we know that the inscribed angle is half of the measure of the intercepted arc.
is an inscribed angle and we know that the inscribed angle is half of the measure of the intercepted arc.
And from the figure arc
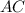 is the intercepted arc.
is the intercepted arc.
Thus, we can write
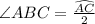
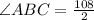

So, the measure of
 .
.
Now given that
 is a tangent to the circle at the point
is a tangent to the circle at the point
 .
.
Thus, we will get
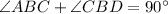
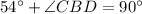
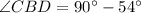
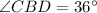
Thus, the measure of the angle
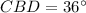 .
.
So, the correct option is A.
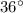 .
.