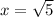Question

To solve y and x, I am adding a picture

Answer 1

`x =\sqrt 5`

`y = \sqrt{5`

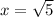
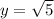
Explanation:

Given

The attached triangle

Required

Solve for x

Considering angle 45 degrees, we have:

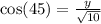`\cos(45) = (y)/(√(10))` --- cosine formula i.e. adj/hyp

Solve for y

`y = √(10) * \cos(45)`

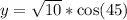
In radical form, we have:

`y = √(10) * (1)/(\sqrt 2)`

`y = √(10/2)`

`y = \sqrt{5`

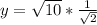
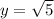
To solve for x, we make use of Pythagoras theorem

`x^2 + y^2 = (√(10))^2`

`x^2 + y^2 =10`

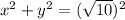
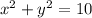
Substitute for y

`x^2 + (\sqrt 5)^2 =10`

`x^2 + 5 =10`

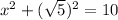
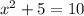
Collect like terms

`x^2 =10-5`

`x^2= 5`

Solve for x

`x =\sqrt 5`