Question

-3x^2-168 solve the quadratic equation

Answer 1

`x=+2i√(14)\ \ \,x=-2i√(14)`

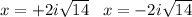
Explanation:

`-3x^2-168`

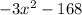
The first step in solving this equation is the factor, remove a factor that both the quadratic and constant term have in common. In this case, such a term would be (-3),

`-3(x^2+56)`

Now set the equation equal to zero so that one can use the zero product property. The zero product property states that any number times zero equals zero.

`-3(x^2+56)=0`

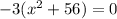
Solve, use inverse operations,

`x^2+56=0`

`x^2=-56`

One cannot take the square root of a negative number and get a real result, thus the result is an imaginary number.

`x=√(-56)`

Simplify, remove whole factors from under the radical,

`x=+-2i√(14)`