Question

Derivative of

`\frac{ {3x}^(2) - 2x - 1 }{ {x}^(2) }`
Show a step.​

Answer 1

`\displaystyle (dy)/(dx) = (2x + 2)/(x^3)`

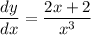
Explanation:

we would like to figure out the derivative of the following:

`\displaystyle \frac{ { 3x }^(2) - 2x - 1 }{ {x}^(2) }`

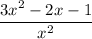
to do so, let,

`\displaystyle y = \frac{ { 3x }^(2) - 2x - 1 }{ {x}^(2) }`

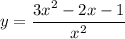
By simplifying we acquire:

`\displaystyle y = 3 - (2)/(x) - \frac{1}{ {x}^(2) }`

use law of exponent which yields:

`\displaystyle y = 3 - 2 {x}^( - 1) - { {x}^( - 2) }`

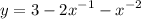
take derivative in both sides:

`\displaystyle (dy)/(dx) = (d)/(dx) (3 - 2 {x}^( - 1) - { {x}^( - 2) } )`

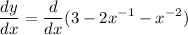
use sum derivation rule which yields:

`\rm\displaystyle (dy)/(dx) = (d)/(dx) 3 - (d)/(dx) 2 {x}^( - 1) - (d)/(dx) {x}^( - 2)`

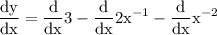
By constant derivation we acquire:

`\rm\displaystyle (dy)/(dx) = 0 - (d)/(dx) 2 {x}^( - 1) - (d)/(dx) {x}^( - 2)`

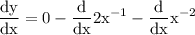
use exponent rule of derivation which yields:

`\rm\displaystyle (dy)/(dx) = 0 - ( - 2 {x}^( - 1 -1) ) - ( - 2 {x}^( - 2 - 1) )`

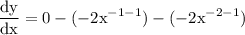
simplify exponent:

`\rm\displaystyle (dy)/(dx) = 0 - ( - 2 {x}^( -2) ) - ( - 2 {x}^( - 3) )`

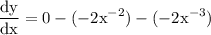
two negatives make positive so,

`\displaystyle (dy)/(dx) = 2 {x}^( -2) + 2 {x}^( - 3)`

further simplification if needed:

by law of exponent we acquire:

`\displaystyle (dy)/(dx) = (2 )/(x^2)+ (2)/(x^3)`

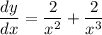
simplify addition:

`\displaystyle (dy)/(dx) = (2x + 2)/(x^3)`

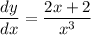
and we are done!