Answer: 8.323 (approximate)
====================================================
Step-by-step explanation:
s = 32 = sample standard deviation
n = 40 = sample size
Despite not knowing the population standard deviation (sigma), we can still use the Z distribution because n > 30. When n is this large, the student T distribution is approximately the same (more or less) compared to the standard Z distribution. The Z distribution is nicer to work with.
At 90% confidence, the z critical value is roughly z = 1.645. This can be found using either a Z table or a calculator.
------------------
We have these values:
- z = 1.645 (approximate)
- s = 32
- n = 40
Plug these values into the margin of error formula.
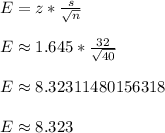
The margin of error is roughly 8.323
I rounded to 3 decimal places because z = 1.645 is rounded to 3 decimal places. If your teacher wants some other level of precision, then be sure to follow those instructions.