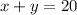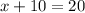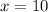Question

You have a babysitting job that pays $6 an hour. You also have

cashier job that pays $9 an hour. You don't want to work more
than 20 hours a week, but you want to make at least $150 a
week. What are the number of hours you can work at each job
and still make at least $150 a week?

Answer 1

One possibility is to work for (10) hours as a babysitter, and (10) hours as a cashier.

Explanation:

An easy way to solve this problem is to set up a system to model the situation. Create one equation to model the money make, and the other to model the time spent. Let parameters (x) and (y) represent the time one spends at each job.

Since one cannot spend more than (20) hours a week working, set the first equation, for time, equal to (20),

x + y = 20

Now multiply each unit for the time by the money earned at each job, set this new equation equal to (150), the minimum amount of money one wishes to earn,

6(x) + 9(y) = 150

Thus the system is the following,

`\left \{ {{x+y=20} \atop {6x+9y=150}} \right.`

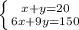
Now use the process of elimination. The process of elimination is when one multiplies one of the equations by a term such that when one adds the two equations, one of the variables cancels. One can solve for the other variable, and then backsolve for the first variable. Multiply the first equation by (-6) so that the variable (x) cancels.

`\left \{ {{-6x-6y=-120} \atop {6x+9y=150}} \right.`

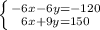
Add the two equations,

`3y=30`

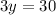
Use inverse operations to solve for (y),

`y=10`

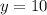
Now substitute the value of (y) back into one of the original equations and solve for (x),

`x+y=20`

`x+10=20`

`x=10`