Given:
The two way table.
To find:
The conditional probability of P(Drive to school | Senior).
Solution:
The conditional probability is defined as:
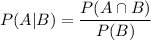
Using this formula, we get
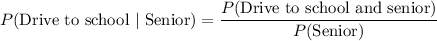 ...(i)
...(i)
From the given two way table, we get
Drive to school and senior = 25
Senior = 25+5+5
= 35
Total = 2+25+3+13+20+2+25+5+5
= 100
Now,
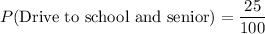
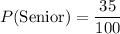
Substituting these values in (i), we get

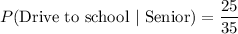
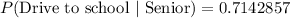
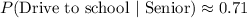
Therefore, the required conditional probability is 0.71.