Question

Please show work, thank you

Answer 1

The instantaneous rate of change of a function let it be f(x) is given by it's first Derivative i.e f'(x) and at a particular point like x = a , it's given by f'(a) . But let's recall a basic formula first :

• 
  `{\boxed{\bf{(d)/(dx)(x^(n))=n{x}^(n-1)}}}`

So , now here ;

`{:\implies \quad \sf f(x)=-4x^(2)+2x}`

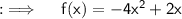
Differentiating both sides w.r.t.x ;

`{:\implies \quad \sf f^(\prime)(x)=-4(d)/(dx)(x^2)+2(dx)/(dx)}`

`{:\implies \quad \sf f^(\prime)(x)=-4\cdot 2 \cdot x+2}`

`{:\implies \quad \sf f^(\prime)(x)=-8x+2}`

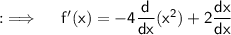
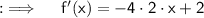
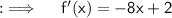
Now , at x = 3 ;

`{:\implies \quad \sf f^(\prime)(3)=-8(3)+2}`

`{:\implies \quad \sf f^(\prime)(3)=-24+2}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{f^(\prime)(3)=-22}}}`

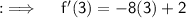
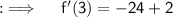
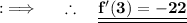
Hence , the required answer is -22