Question

The side of a given cube is n units in length. If this length is tripled, how would the volume of the new cube compare to the volume of the original cube?

Answer 1

Option 4

Explanation:

Points to remember to solve this question,

1). Dimension scale factor of the cube =
`\frac{\text{Dimension of the image}}{\text{Dimension of the original}}`

2). Volume scale factor the cube =
`\frac{\text{Volume of the image}}{\text{Volume of the original}}`

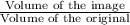
3). Volume scale factor = (Dimension scale factor)³

Since, length of the cube = n units

Length of the cube after dilation = 3n units

Dimension scale factor =
`(3n)/(n)=3`

Volume scale factor = (Dimension scale factor)³

= (3)³

= 27

Since, Volume scale factor the cube =
`\frac{\text{Volume of the image}}{\text{Volume of the original}}`

`\frac{\text{Volume of the image}}{\text{Volume of the original}}=27`

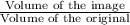
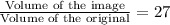
Volume of the image cube = 27(Volume of the original cube)

Therefore, Option 4 will be the answer.