Question

A gas with a volume of 250 mL at a temperature of 293K is heated to 324K. What is the new volume of the gas?

Answer 1

The new volume of the gas is 276.45 mL.

Step-by-step explanation:

Charles's law indicates that for a given sum of gas at constant pressure, as the temperature increases, the volume of the gas increases, and as the temperature decreases, the volume of the gas decreases.

Charles's law is a law that mathematically says that when the amount of gas and pressure are kept constant, the quotient that exists between the volume and the temperature will always have the same value:

`(V)/(T) =k`

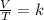
Analyzing an initial state 1 and a final state 2, it is satisfied:

`(V1)/(T1) =(V2)/(T2)`

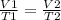
In this case:

• V1= 250 mL
• T1= 293 K
• V2= ?
• T2= 324 K

Replacing:

`(250 mL)/(293 K) =(V2)/(324 K)`

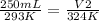
Solving:

`V2=324 K*(250 mL)/(293 K)`

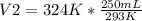
V2= 276.45 mL

The new volume of the gas is 276.45 mL.