Question

A consulting firm submitted a bid for a large research project. The firm's management initially felt they had a chance of getting the project. However, the agency to which the bid was submitted subsequently requested additional information on the bid. Past experience indicates that for of the successful bids and of the unsuccessful bids the agency requested additional information. a. What is the prior probability of the bid being successful (that is, prior to the request for additional information) (to decimal)? b. What is the conditional probability of a request for additional information given that the bid will ultimately be successful (to decimals)? c. Compute the posterior probability that the bid will be successful given a request for additional information (to decimals).

Answer 1

Explanation:

Dear student, the missing data in the given information includes that:

The past experience showcases that for 75% successful bids & 40% unsuccessful bids, additional information is being requested by the agency.

∴

For a bid to be successful, the chance is half

Thus, the prior probability P(successful) is;

P(successful) =
`(50)/(50+50)`

P(successful) = 0.5

The conditional probability is:

`P(request/successful)= (P(request \& \ successful) )/(P(successful))`

`P(request/successful)= 0.75`

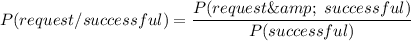
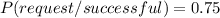
To compute the posterity probability, we use the Naive Bayes Theorem:

So,

Let S = successful, Us = Unsuccessful; R = request:

Then;

`P(S/R) = (P(R/S) *P(S))/([P(R/s)* P(S) +P(R/Us) *P(Us)])`

`P(S/R) = (0.75*0.5)/(0.75* 0.5 +0.40 *0.5])`

`P(S/R) = (0.375)/(0.375 +0.20) \\ \\ P(S/R) = (0.375)/(0.575)`

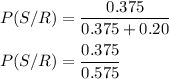
P(S/R) = 0.65