Question

The variable y is calculated by multiplying the variable of x by 2. There is a third variable (variable z), and it is known that the correlation of z with x is .45. What is the correlation of z with y

Answer 1

The correlation between two variables, let's say A and B, is given by:

`r(A.B) = \frac{ \sum{A*B}}{ \sqrt{\sum{A^2}* \sum{B^2}}}`

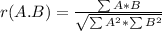
In our case, we know that:

y = 2*x

And:

r(X, Z) = 0.45

Then:

Now we want to find:

r(Y, Z)

Let's start with r(X, Z)

We know that:

X = Y/2

Then we can replace that in the correlation equation:

`r(X.Z) = \frac{ \sum{X*Z}}{ \sqrt{\sum{X^2}* \sum{Z^2}}} = 0.45 \\`

`r(Y/2.Z) = \frac{ \sum{(Y/2)*Z}}{ \sqrt{\sum{(Y/2)^2}* \sum{Z^2}}} = 0.45 \\`

`r(Y/2, Z) = \frac{ (1/2)*\sum{Y*Z}}{\sqrt{ (1/4)\sum{(Y)^2}* \sum{Z^2}}} = \frac{ \sum{(Y)*Z}}{ \sqrt{\sum{(Y)^2}* \sum{Z^2}}} = 0.45`

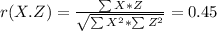
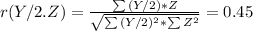
And in the third part, we have r(Y,Z), then:

`r(Y, Z) = \frac{\sum{Y*Z}}{\sqrt{\sum{Y^2}*\sum{Z^2}}} = 0.45`

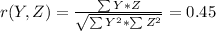
The correlation of z with y is 0.45