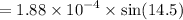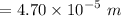Solution :
Given :
The angle of the first maximum with the center is given by :
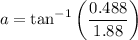
= 14.5°
The grating distance can be calculated as :

=

When the principal maxima yields at y = 0.488 m and the length from the wall 1.88 m. Thus the equation of the wavelength is :
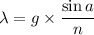 , where n = 1
, where n = 1