Question

A computer laboratory manager was in charge of purchasing new battery packs for her lab of laptop computers. She narrowed her choices to two models that were available for her machines. Since the models cost about the same, she was interested in determining whether there was a difference in the average time the battery packs would function before needing to be recharged. She took two independent samples and computed the following summary information: The test statistic is: -0.7557 Using alpha

Answer 1

The information is missing. The information is :

Battery Pack model 1 Battery Pack model 2

Sample size 9 9

Sample mean 5 hours 5.5 hours

Standard deviation 1.5 hours 1.3 hours

Solution :

Given :

`$n_1 = 9, x_1 = 5,s_1 = 1.5$`

`$n_2 = 9, x_2 = 5.5 ,s_2 = 1.3$`

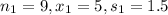
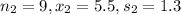
The null hypothesis is :

`$H_0: \mu_1-\mu_2=0$`

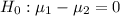
The alternate hypothesis is :

`$H_a: \mu_1-\mu_2 \\eq0$`

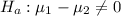
Therefore, the standard error is

`$SE = \sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2)}$`

`$ = \sqrt{(1.5^2)/(9)+(1.3^2)/(9)}$`

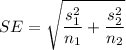
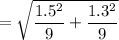
= 0.66165

Thus the test statics is

`$t=(x_1-x_2)/(SE)$`

`$t=(5-5.5)/(0.66165)$`

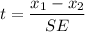
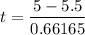
= -0.756