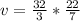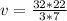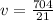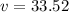Answer:
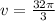
or
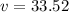
Explanation:
Given
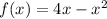
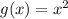
![[a,b] = [0,2]](https://img.qammunity.org/2022/formulas/mathematics/college/fhi3gzigbjhoyblmlva73gq9tffaom6t7r.png)
Required
The volume of the solid formed
Rotating about the x-axis.
Using the washer method to calculate the volume, we have:
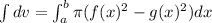
Integrate
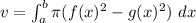
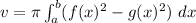
Substitute values for a, b, f(x) and g(x)
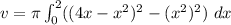
Evaluate the exponents
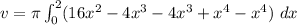
Simplify like terms
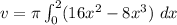
Factor out 8
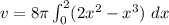
Integrate
![v = 8\pi [ (2x^(2+1))/(2+1) - (x^(3+1))/(3+1) ]|\limit^2_0](https://img.qammunity.org/2022/formulas/mathematics/college/qd4zu1bpfkl0xl81iuazr4drp4gg3hg13m.png)
![v = 8\pi [ (2x^(3))/(3) - (x^(4))/(4) ]|\limit^2_0](https://img.qammunity.org/2022/formulas/mathematics/college/n62s41gb07tt1dnpsiz5ske64gowg3d3ex.png)
Substitute 2 and 0 for x, respectively
![v = 8\pi ([ (2*2^(3))/(3) - (2^(4))/(4) ] - [ (2*0^(3))/(3) - (0^(4))/(4) ])](https://img.qammunity.org/2022/formulas/mathematics/college/l7s9p010wqoelb3doayze1rxluimyuug1s.png)
![v = 8\pi ([ (2*2^(3))/(3) - (2^(4))/(4) ] - [ 0 - 0])](https://img.qammunity.org/2022/formulas/mathematics/college/kdcifn4di7on2sn2tzlf7vwwieocugybnw.png)
![v = 8\pi [ (2*2^(3))/(3) - (2^(4))/(4) ]](https://img.qammunity.org/2022/formulas/mathematics/college/h1vr4efpp22jwsc2uyvjb8v5q0nd0fbn6e.png)
![v = 8\pi [ (16)/(3) - (16)/(4) ]](https://img.qammunity.org/2022/formulas/mathematics/college/l28xxtwzn5oynuvva7bepcvhq7ztxve5n7.png)
Take LCM
![v = 8\pi [ (16*4- 16 * 3)/(12)]](https://img.qammunity.org/2022/formulas/mathematics/college/il5aybvmd1vmg9l02llja91lf8y67ewwrj.png)
![v = 8\pi [ (64- 48)/(12)]](https://img.qammunity.org/2022/formulas/mathematics/college/ms16wtlg9yaxvechp1jznx2bxid736ffpu.png)
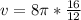
Simplify
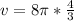
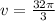
or