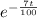Answer:
a. dS(t)/dt + [7S(t)/(300 - 5t)] = 1.2 with S(0) = 0.8
b. S(t) =
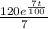 - 16.34
- 16.34
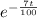
Explanation:
a. Write an initial value problem for S(t), the amount of salt in the tank at time t. Do not solve the equation!!
The net mass flow rate of salt dS(t)/dt = mass flow in - mass flow out
mass flow in = concentration of flow in × flow rate in = 0.6 lb/gal × 2 gal/min = 1.2 lb/min
Let S(t) be the mass of salt in the tank at time, t. The concentration of salt in the tank at time, t, C(t) = S(t)/volume of tank at time t ,V
V = V₀ + (r - r')t where V₀ = initial volume of water in tank = 300 gal, r = volume flow rate in = 2 gal/min, r'= volume flow rate out = 7 gal/min and t = time
So, V = V₀ + (r - r')t
V = 300 + (2 - 7)t
V = 300 - 5t
So, C(t) = S(t)/V = S(t)/(300 - 5t) lb/gal
Now, mass flow rate out = concentration in tank × volume flow rate out = S(t)/(300 - 5t) lb/gal × 7 gal/min = 7S(t)/(300 - 5t) lb/min
So, dS(t)/dt = mass flow in - mass flow out
dS(t)/dt = 1.2 lb/min - 7S(t)/(300 - 5t) lb
dS(t)/dt = 1.2 - 7S(t)/(300 - 5t)
So, our differential equation is
dS(t)/dt + [7S(t)/(300 - 5t)] = 1.2 with S(0) = 0.8 since we initially have 0.8 lb of salt
b. Write an expression in terms of S for the amount of salt in the tank when the tank is one-quarter full.
When the tank is one-quarter full, V = volume of tank/4 = 400 gallons/4 = 100 gallons
We now solve our differential equation
dS(t)/dt + 7S(t)/100 = 1.2
Using the integrating factor method, I.F =
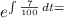

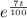 dS(t)/dt +
dS(t)/dt +
d[
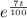 S(t)]/dt = 1.2
S(t)]/dt = 1.2
d[
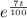 S(t)] = [1.2
S(t)] = [1.2
integrating both sides, we have
∫d[
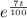 S(t)] = ∫[1.2
S(t)] = ∫[1.2
Let u = 7t/100. So, du/dt = 7/100 and dt = 100du/7
∫[1.2
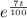 ]dt = ∫[1.2 × 100
]dt = ∫[1.2 × 100
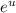 ]du/7 = (120/7)∫
]du/7 = (120/7)∫
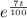 S(t) =
S(t) =
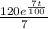 + C
+ C
S(t) =
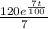 ÷
÷
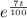 +
+
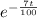
S(t) =
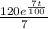 + C
+ C
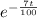
From our initial condition, S(0) = 0.8. So,
S(0) =
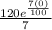 + C
+ C
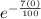
S(0) =
 + C
+ C
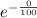
S(0) =
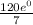 + C
+ C
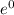
0.8 =
 + C
+ C
C = 0.8 - 120/7
C = 0.8 - 17.14
C = - 16.34
So,
S(t) =
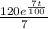 - 16.34
- 16.34