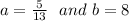Answer:
Line A passes through (-3, 2) and (-23, 54)
slope of line A will be
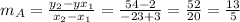
Equation of line A will be
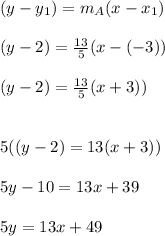
Given line B is parallel to line A, So slope of A and B
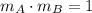
slope of line B will be
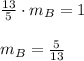
Also given line B passes (-8, 0), therefore the equation of line B
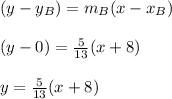
Therefore,