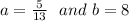Question

Line A passes through the points (-3,2) and (-23,54). Line B is parallel to line A and passes through the point (-8,0). Consider

the equation of line B in the form y= a (x + b), where a and b are rational numbers.

Answer 1

Line A passes through (-3, 2) and (-23, 54)

slope of line A will be

`m_(A) =(y_(2)-yx_(1) )/(x_(2)- x_(1) ) = (54-2)/(-23+3) = (52)/(20)= (13)/(5)`

Equation of line A will be

`(y - y_(1)) = m_(A)(x-x_(1) )\\\\(y - 2) = (13)/(5)(x -(-3))\\\\(y - 2) = (13)/(5)(x +3))\\ \\\\5((y - 2) = 13(x +3))\\\\5y -10 = 13x + 39\\\\5y = 13x + 49`

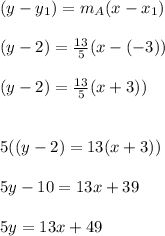
Given line B is parallel to line A, So slope of A and B

`m_(A) \cdot m_(B) = 1`

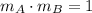
slope of line B will be

`(13)/(5)\cdot m_(B) = 1\\\\m_(B) = (5)/(13)`

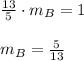
Also given line B passes (-8, 0), therefore the equation of line B

`(y-y_(B)) = m_(B)(x-x_(B) )\\\\(y - 0) = (5)/(13)(x + 8)\\\\y = (5)/(13)(x+8)\\\\`

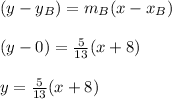
Therefore,

`a = (5)/(13) \ \ and \ b = 8`