Answer:
Bias for the estimator = -0.56
Mean Square Error for the estimator = 6.6311
Explanation:
Given - A normally distributed random variable with mean 4.5 and standard deviation 7.6 is sampled to get two independent values, X1 and X2. The mean is estimated using the formula (3X1 + 4X2)/8.
To find - Determine the bias and the mean squared error for this estimator of the mean.
Proof -
Let us denote
X be a random variable such that X ~ N(mean = 4.5, SD = 7.6)
Now,
An estimate of mean, μ is suggested as
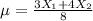
Now
Bias for the estimator = E(μ bar) - μ
=
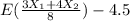
=
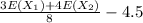
=
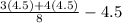
=
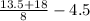
=
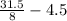
= 3.9375 - 4.5
= - 0.5625 ≈ -0.56
∴ we get
Bias for the estimator = -0.56
Now,
Mean Square Error for the estimator = E[(μ bar - μ)²]
= Var(μ bar) + [Bias(μ bar, μ)]²
=
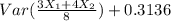
=
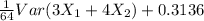
=
![(1)/(64) ( [{3Var(X_(1)) + 4Var(X_(2))] }) + 0.3136](https://img.qammunity.org/2022/formulas/mathematics/college/gtzbromru4xvut53czpgsfbda8y2jykpcy.png)
=
![(1)/(64) [{3(57.76) + 4(57.76)}] } + 0.3136](https://img.qammunity.org/2022/formulas/mathematics/college/spjwcqgmpxsnxify7a9dj8jm8r95qtqjpe.png)
=
![(1)/(64) [7(57.76)}] } + 0.3136](https://img.qammunity.org/2022/formulas/mathematics/college/or88usi306lvcte2x674emwtx77v12pzw5.png)
=
![(1)/(64) [404.32] } + 0.3136](https://img.qammunity.org/2022/formulas/mathematics/college/35rx76i2mvpujs6alfl8re89kqgzkkgnes.png)
=
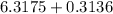
= 6.6311
∴ we get
Mean Square Error for the estimator = 6.6311