Question

An electron is constrained to the central perpendicular axis of a ring of charge of radius 2.2 m and charge 0.021 mC. Suppose the electron is released from rest a distance 0.050 m from the ring center. It then oscillates through the ring center. Calculate its period. (The electron is always much closer to the ring center than a radius.)

Answer 1

T = 1.12 10⁻⁷ s

Step-by-step explanation:

This exercise must be solved in parts. Let's start looking for the electric field in the axis of the ring.

All the charge dq is at a distance r

dE = k dq / r²

Due to the symmetry of the ring, the field perpendicular to the axis is canceled, leaving only the field in the direction of the axis, if we use trigonometry

cos θ =
`(dE_x)/(dE)`

dEₓ = dE cos θ

cos θ = x / r

substituting

dEₓ =
`k (dq)/(r^2 ) \ (x)/(r)`

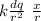
DEₓ = k dq x / r³

let's use the Pythagorean theorem to find the distance r

r² = x² + a²

where a is the radius of the ring

we substitute

dEₓ =
`k (x)/((x^2 + a^2 ) ^(3/2) ) \ dq`

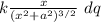
we integrate

∫ dEₓ =k \frac{x}{(x^2 + a^2 ) ^{3/2} } ∫ dq

Eₓ =
`k \ Q \ (x)/((x^2+a^2)^(3/2))`

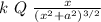
In the exercise indicate that the electron is very central to the center of the ring

x << a

Eₓ =
`k \ Q (x)/(a^3 \ ( 1 +(x/a)^2)^(3/2)))`

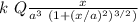
if we expand in a series

`(\ 1+ (x/a)^2 \ )^(-3/2) = 1 - (3)/(2) ((x)/(a) )^2`

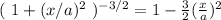
we keep the first term if x<<a

Eₓ =
`( k Q)/(a^3) \ x`

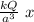
the force is

F = q E

F =
`- (kQ )/(a^3) \ x`

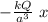
this is a restoring force proportional to the displacement so the movement is simple harmonic,

F = m a

`- (keQ)/(a^3) \x = m (d^2 x)/(dt^2 )`

`(d^2 x)/(dt^2) = (keQ)/(ma^3) \ x`

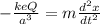
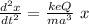
the solution is of type

x = A cos (wt + Ф)

with angular velocity

w² =
`(keQ)/(m a^3)`

angular velocity and period are related

w = 2π/ T

we substitute

4π² / T² = \frac{keQ}{m a^3}

T = 2π
`\sqrt{(m a^3 )/(keQ) }`

let's calculate

T = 2π
`\sqrt{ ( 9.1 \ 10^(-31) \ 2.2^3 )/(9 \ 10^9 \ 1.6 \ 10^(-19) \ 0.021 \ 10^(-3) ) }`

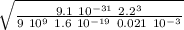
T = 2π pi
`\sqrt{320.426 \ 10^(-18) }`

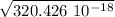
T = 2π 17.9 10⁻⁹ s

T = 1.12 10⁻⁷ s