Answer:
The 90% confidence interval for the population proportion of all such firms with this as the primary motivation is (69.96%, 80.04%).
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
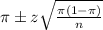
In which
z is the z-score that has a p-value of
 .
.
The Corporate Lawyer, a magazine for corporate lawyers, reported that out of 200 firms with employee stock ownership plans, 150 indicated that the primary reason for setting up the plan was tax related.
This means that
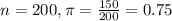
90% confidence level
So
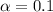 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
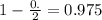 , so
, so
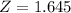 .
.
The lower limit of this interval is:
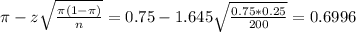
The upper limit of this interval is:
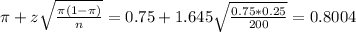
As percent:
0.6996*100% = 69.96%
0.8004*100% = 80.04%.
The 90% confidence interval for the population proportion of all such firms with this as the primary motivation is (69.96%, 80.04%).