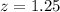Answer:
The test statistic is
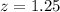
Explanation:
We are interested in determining whether or not the proportion of the student who experience anxiety during the exam is significantly more than 80%.
At the null hypothesis, we test if the proportion is 80%, that is:
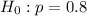
At the alternate hypothesis, we test if the proportion is more than 80%, that is:

The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
80% is tested at the null hypothesis:
This means that

A random sample of 100 students was taken. Eighty-five of the student in the sample experienced anxiety during the exam.
This means that
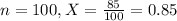
The test statistic is

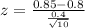
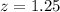
The test statistic is